Click here👆to get an answer to your question ️ If g(x) = x^2 x 1 and (gof)(x) = 4x^2 10x 5 , then f (54) is equal to Join / Login > 12th > Maths > Relations and Functions > Composition of Functions > If g(x) = x^2 x 1 and ( maths If g (x) = x 2 x − 1 and (g o f) (x) = 4 x 2 − 1 0 x 5, then f (4 5 ) is equal to A 2 3 B 2 1 C − 2 3 D − 2 1 Hard AnswerI assume you know how to graph For each value of x the point on f (x) = x^2 4 is 4 units below the point with the same x value on g (x) = x^2 so take the graph of g (x) and move it down 4 units to obtain the graph of f (x) I'm confused by second part of your question IIf f(x) = 2x^3 3x^2 4x 1 and g(x) =3
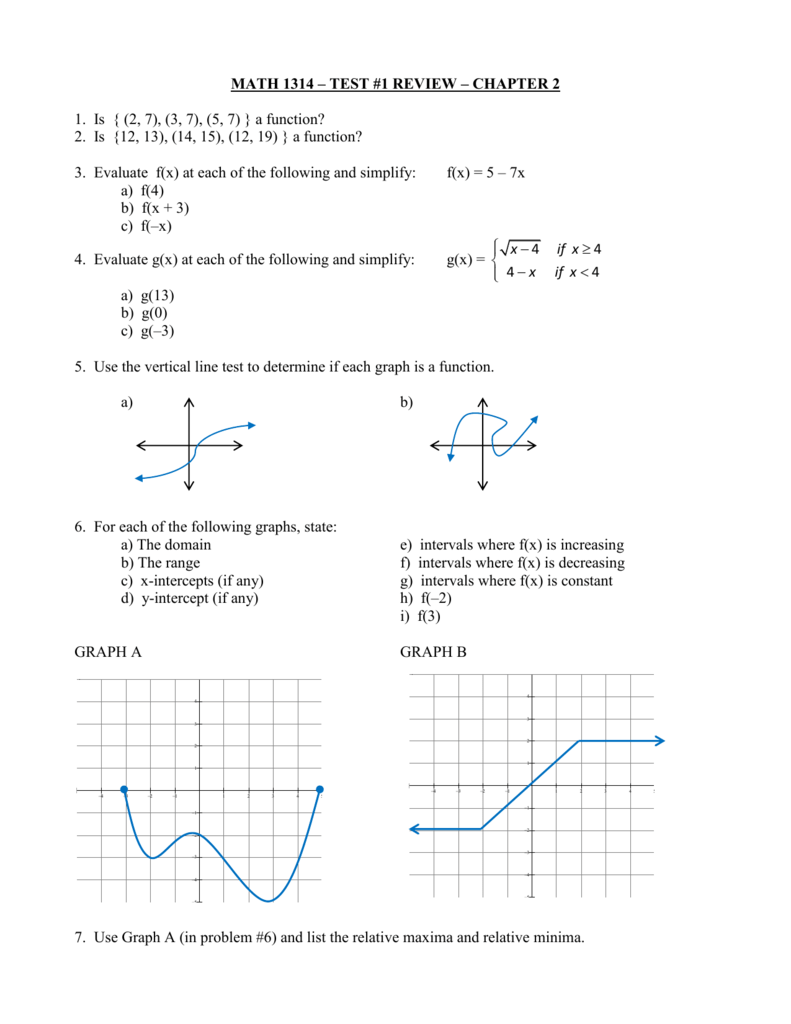
Test 1 Review
If f(g(x))=ln(x^2+4)
If f(g(x))=ln(x^2+4)-2 Why is there a "break" in the line at x=2?(2\times1) (3\times1) (4\times1) (5\times1) (6\times1) (7\times1) \mathrm{Radians} \mathrm{Degrees} \square!




Solved 1 If G 5 3 G 5 6 H 5 3 And H 5 Chegg Com
This is a composite function Concept For such a function, ie g(f(x)), perform inner, and then outer This means evaluate f(x) first The value will be known as value V Then perform g(V) Essentially, g(f(x))= g(V), where f(x)= V where x and VWhy is the graph a line without a vertical asymptote at x=2?Given f(x) = 2x 3 and g(x) = –x 2 5, find (g o g)(1) (g o g)(1) = g(g(1)) = g(–( ) 2 5) setting up to insert the original input = g(–(1) 2 5) = g(–1 5) = g(4) = –( ) 2 5 setting up to insert the new input = –(4) 2 5 = –16 5 = –11 In each of these cases, I wrote out the steps carefully, using parentheses to indicate where my input was going with respect
· If f(x) = 2x 3 and f(g(x)) = 8x – 1, which of the following equals g(x)?1)Graph f(x)=(x^2 4)/(x 2) using a graphing calculator Using a standard window with the trace feature, trace the graph to x=2 What happens?(a) f ( x) = 6 , g ) =3 (b) f(x 2, g(x) = 4x (c) f(x) = 2x, g(x) = x2 (d) f(x) = x4, g(x) = ex (e) f(x) = x1, g(x) = x2 4 (a) domain is all real x, range is −1 ≤ y ≤ 1 (b) domain is all real x, range is y ≥ 1 (c) domain is x < 0, range is all real y (d) domain is x 6= 0 , range is −2 ≤ y ≤ 2 wwwmathcentreacuk 5 c mathcentre 09 Title mcTYcomposite091dvi Created
Since (x1)(x4) = 0 for x=1 and x=4 , function f is continuous for all values of x EXCEPT x=1 and x=4 Click HERE to return to the list of problems SOLUTION 7 First describe function g using functional composition Let f(x) = x 1/3, , and k(x) = x 5 Function k is continuous for all values of x since it is a polynomial, and functions f and h are wellknown to be continuous for allX (3x ) View solution steps Solution Steps F ( x ) = 3 x ^ { 2 } 5 x ( 4 ) F ( x) = 3 x 2 − 5 x ( − 4) Multiply 5 and 4 to get Multiply 5 and − 4 to get − 2 0 3x^ {2}\left (x\right) 3 x 2 − ( − 2 0 x) · In order to find what value (x) makes f (x) undefined, we must set the denominator equal to 0, and then solve for x f (x)=3/ (x2);




In Exercises 27 32 Use Theorem 2 To Calculate 8 X Chegg Com




If F X 3x 4 And G X 2 Solve For The Value Of X For Which F X G X Is True Brainly Com
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and capabilities to the broadest possible/12/16 · The answers are f(g(x))=x^21 and g(f(x))=(x3)^24 This is a composition of functions f(x)=x3 g(x)=x^24 f(g(x))=f(x^24)=x^243=x^21 The range is f(g(x)) in 1, oo g(f(x))=g(x3)=(x3)^24 The range is g(f(x)) in 4, ooPrecalculus Science Anatomy & Physiology Astronomy Astrophysics Biology Chemistry Earth Science Environmental ScienceGiven f (x) = 2x, g(x) = x 4, and h(x) = 5 – x 3, find (f g)(2), (h – g)(2), (f × h)(2), and (h / g)(2) This exercise differs from the previous one in that I not only have to do the operations with the functions, but I also have to evaluate at a particular xvalue To find the answers, I can either work symbolically (like in the previous example) and then evaluate, or else I can find



If F X F G X Where F 4 3 F 4 7 F Chegg Com



94 5 8 8 X 7 4 6 H X 3 Y Values Y Values 2 3 2 1 1 Chegg Com
MATH COMPOSITION FUNCTIONS KSU Deflnition † Composition function Given two functions f and g, the composition function f –g is deflned by (f –g)(x) = f(g(x))In other words, given a number x, we flrst apply g to it and then we apply f to the result Here, f is the outside function and g is the inside function Important Properties † Let c be any constantFor instance, when D is applied to the square function, x ↦ x 2, D outputs the doubling function x ↦ 2x, which we named f(x) This output function can then be evaluated to get f(1) = 2, f(2) = 4, and so on Higher derivatives Let f be a differentiable function, and let f ′ be its derivativeA composite function is a function which is made by combining two or more than two functions For example, if f(x) f ( x) and g(x) g ( x) are two functions, then we can define two composite




Mcdonnell Douglas F 4 Phantom Ii Wikipedia



Answered 5 8 4 H X 7 G X 5 4 3 3 Bartleby
· If #f(x) = x^24# and #g# is a differentiable function of #x#, what is the derivative of #f(g(x))#?Given the function f (xEthanorford ethanorford Mathematics High School answered F(x) = x 2 g(x) = x – 4 (f g)(x) = 2 See answers riqueeybarra riqueeybarra (x2)*(x4) x^24x2x8 x^22x8 keyalaboyd keyalaboyd x^2 2x 8 is the answer New questions in Mathematics A squirrel moved 0 meters in 7,0
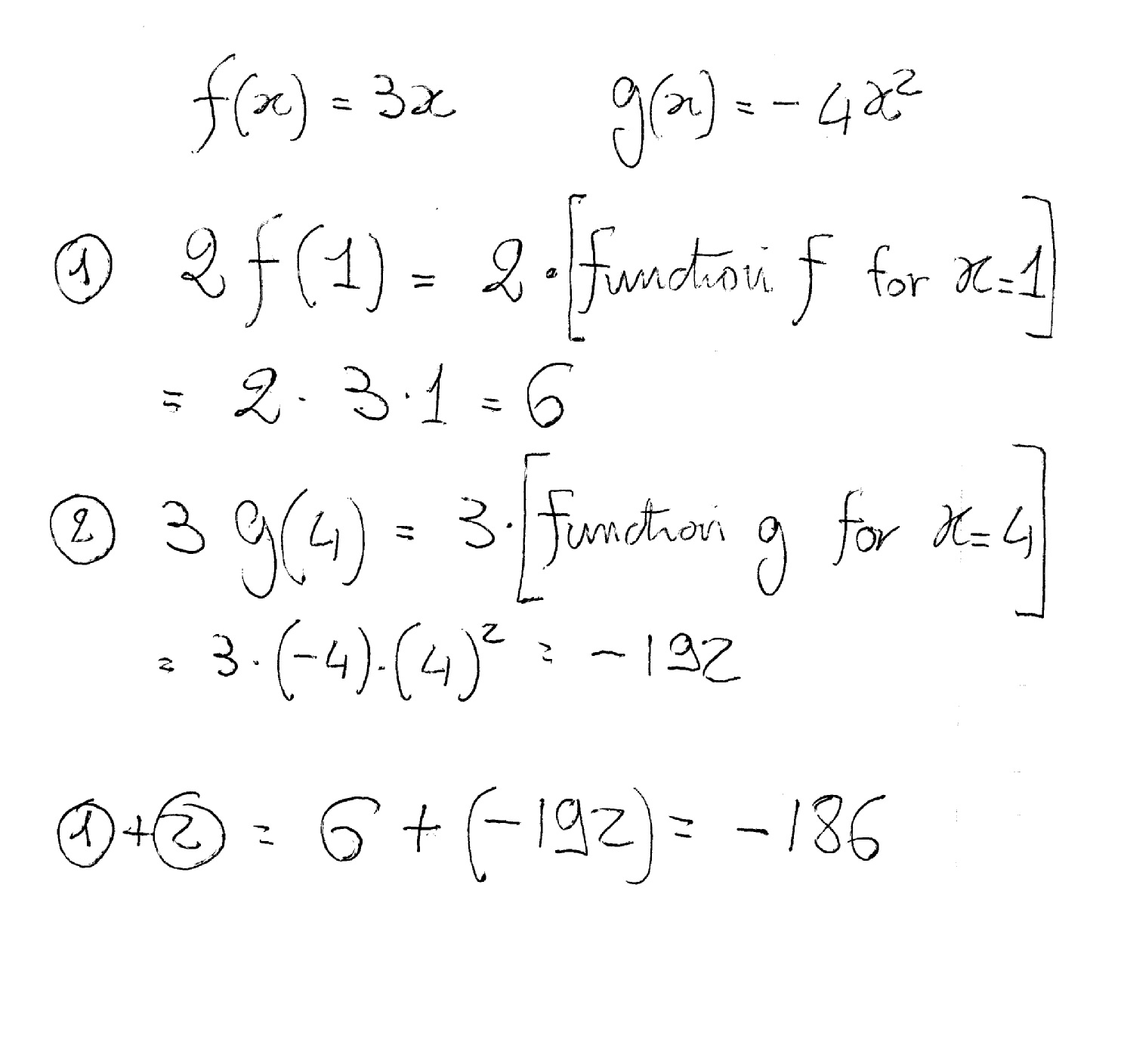



How Do Find The Value Of 2f 1 3g 4 If F X 3x And G X 4x 2 Socratic




Solved 1 If G 5 3 G 5 6 H 5 3 And H 5 Chegg Com
The Algebra of Functions Like terms, functions may be combined by addition, subtraction, multiplication or division Example 1 Given f ( x ) = 2x 1 and g ( x ) = x2 2x – 1 find ( f g ) ( x ) and ( f g ) ( 2 ) · Find (f∘g) (−4) for the following functions f (x)=4x−2 and 1 Use the Intermediate Value Theorem to show that the 1 Use the Intermediate Value Theorem to show that the equation cosx = x^2 has at least one solution you do not need to find the solution2 If 4x 9 is read more% \mathrm{clear} \arcsin \sin \sqrt{\square} 7 8 9 \div \arccos \cos \ln 4 5 6 \times \arctan \tan \log 1 2 3\pi e x^{\square} 0 \bold{=} Go Related » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep




Let 𝑓 𝑥 03 50 If 𝑥 Lt 4 If 4 𝑥 Lt 1 If Chegg Com




F 4 If G X 2 X Brainly Com
X → Function → y A letter such as f, g or h is often used to stand for a function The Function which squares a number and adds on a 3, can be written as f(x) = x 2 5 The same notion may also be used to show how a function affects particular values Example f(4) = 4 2 5 =21, f(10) = (10) 2 5 = 105 or alternatively f x → x 2 5We set the denominator,which is x2, to 0 (x2=0, which is x=2) When we set the denominator of g (x) equal to 0, we get x=0 So x cannot be equal to 2 or 0 Please click on the image for a better understandingFor the given functions of each composite functions f and g, find f of g, g of f, f of f, g of g




If F X X 2 7 X 4 P G X X 2 Q X 4 9 And The Lcm Of F X And G X Is X 2 Q X 4 Youtube
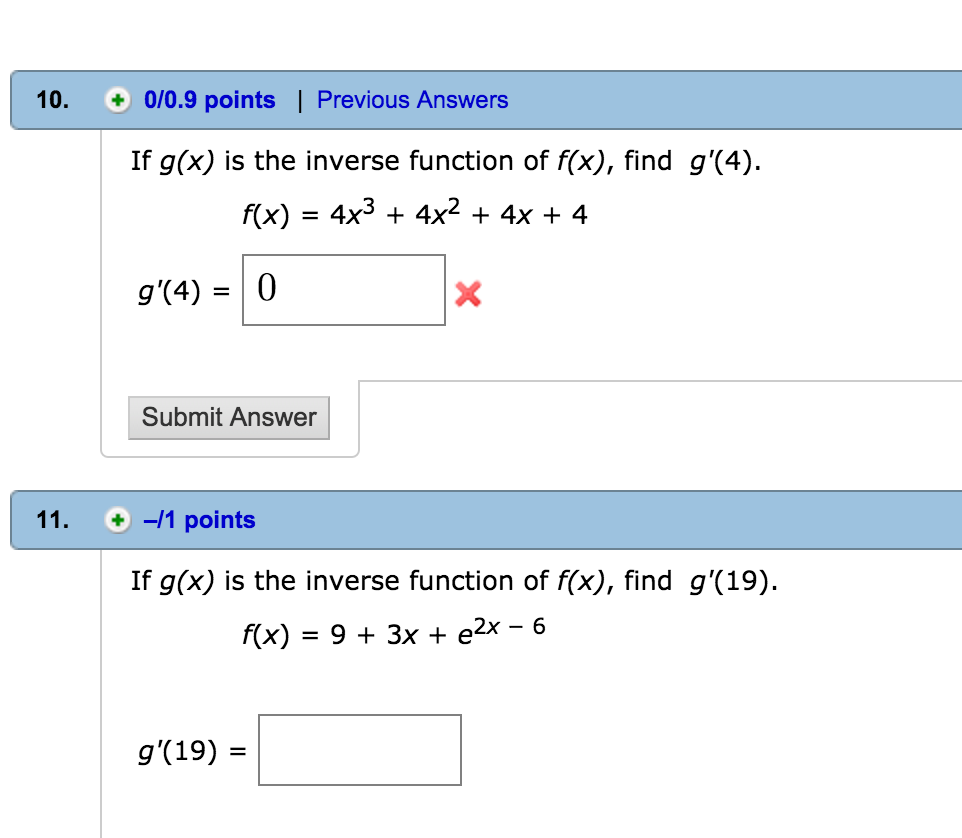



If G X Is The Inverse Function Of F X Find Chegg Com
Solution for If f(x) = (1 − x)2 and g(x) = 4 − x, find f(g(x)) and g(f(x)) Q Assume that the probability of the birth of a child of a particular sex is 50%In a family with six A Probability of girl = 05 Probability of boy = 05 Also the birth of boy and girl is independentI'm a little stuck with this simple function If ${f(g(x)) = 4x^28x}$ and ${f(x)=x^24}$, then what's the value of ${g(x)?}$ Any tips?F (x) = x2 − 4 f (x) = x 2 4 ;
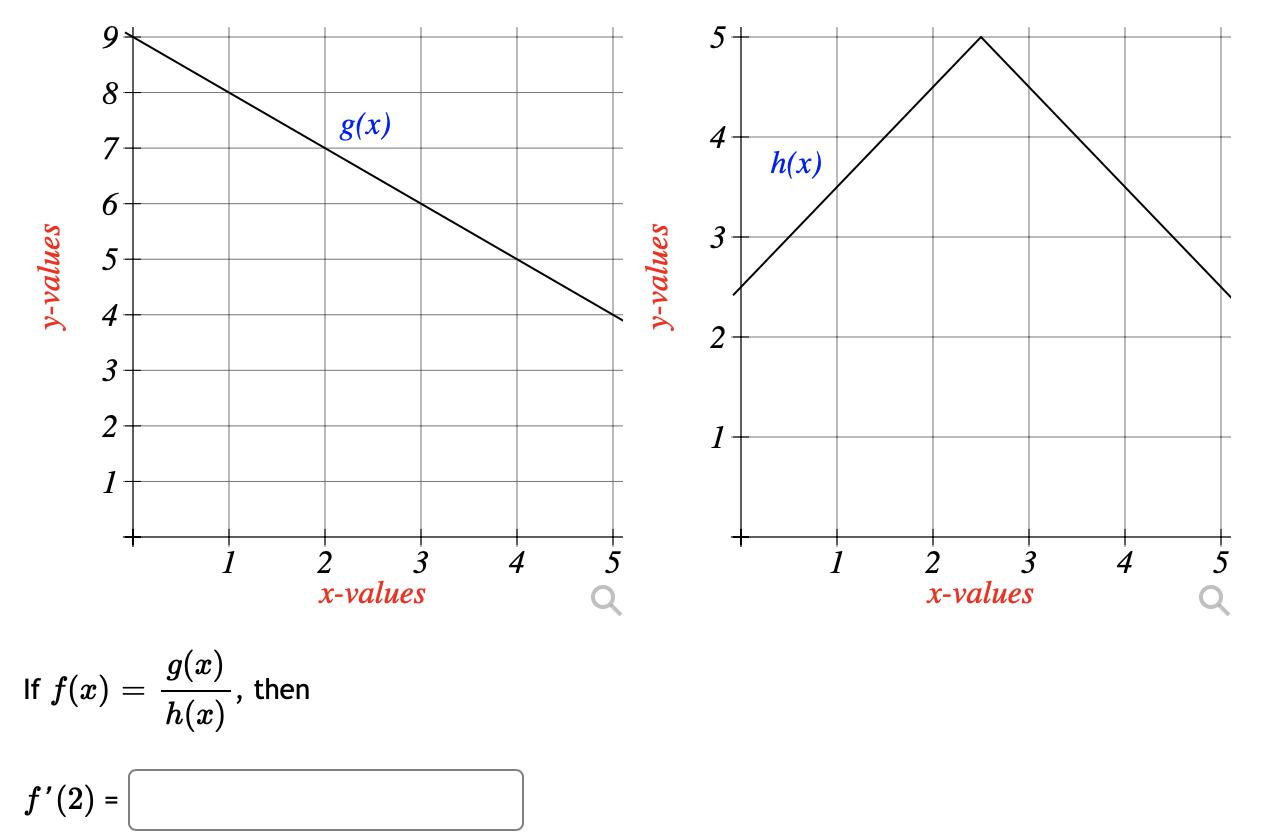



Answered 9 5 8 G X 4 H X 7 6 3 5 2 3 2 1 1 Bartleby
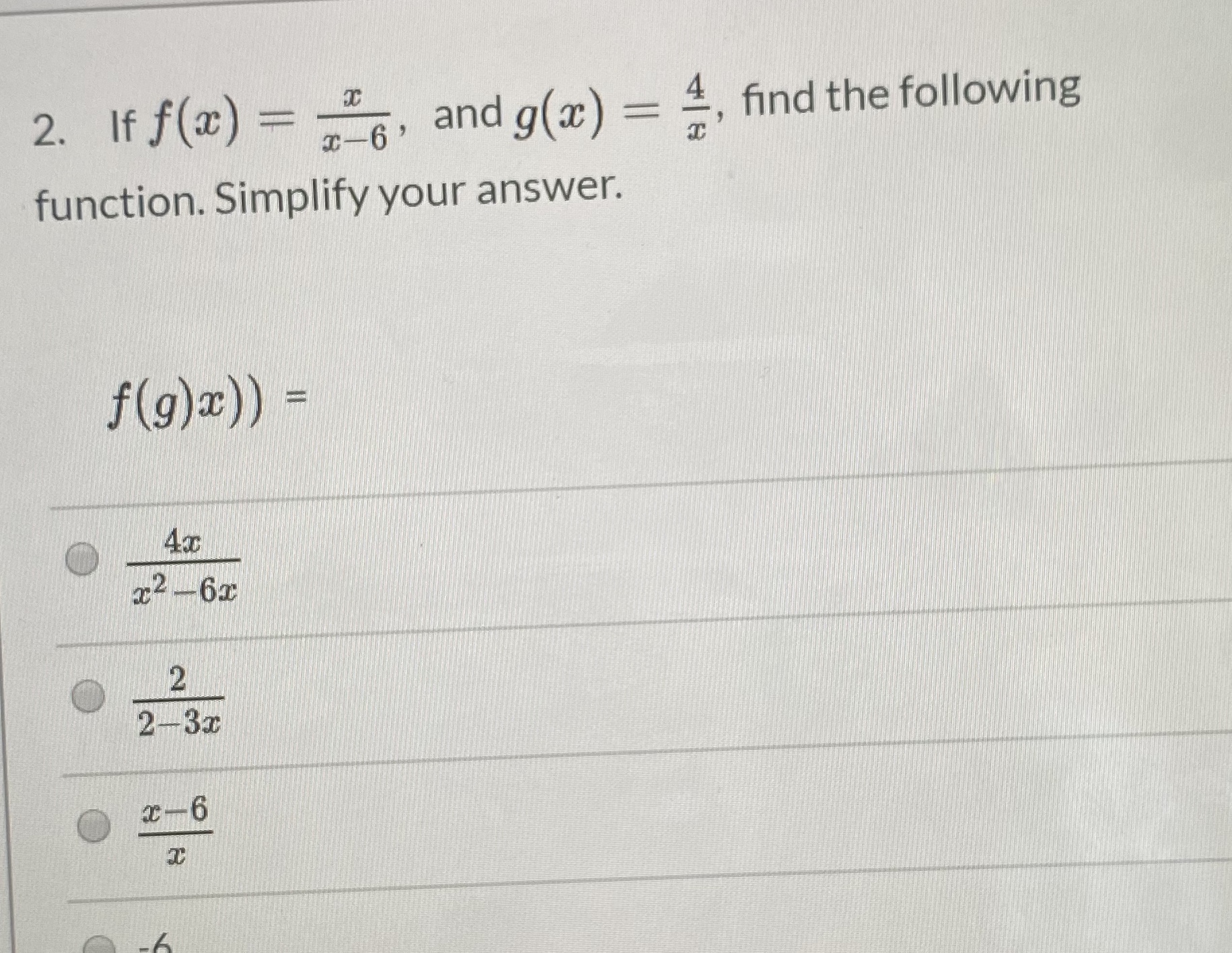



Answered 2 If F X And G X 4 Find The Bartleby
· If g(x) = x2 x 1 and (gof)(x) = 4x2 10x 5, then f(5/4) is equal to (1) 3/2 (2) 1/2 (3) 3/2 (4) 1/2 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!G(x)=f(x2) No solutions found Rearrange Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation g*(x)(f*(x2))=0 Given the function \displaystyle{f{{\left({x}\right)}}}={x}²{3}{x}{1} , how do you determine whether f satisfies the hypotheses of the Mean Value Theorem on the interval 1,1 and find the c?




Function Notation For Sat Math What You Need To Know Youtube




If G X 2x 1 And H X 4x 2 4x 7 Find A Function F Such That F O G H
We now look at the functions f(x) = and g(x) = 4 – x 2 and find the domain and range of their composite functions We obviously have to limit the values under the squareroot sign to non negative numbers only Therefore the composite function f(g(x)) = can only take the positive values that we get from the function g(x) = 4 – x 2 This means we have to limit the domain of the inner · If g(x) = x2 x – 1 and g(f(x)) = 4x2 – 10x 5, then find f (5/4) (1) 1/2 (2) 1/2 (3) 1/3 (4) 1/3 The value of c in the Lagrange's mean value theorem for the function f(x) = x^3 – 4x^2 8x 11, when x ∈ 0, 1 isProof of f(x) g(x) = f(x) g(x) from the definition We can use the definition of the derivative




F 4 1 If G X 2 X Brainly Com




If F X 3x 10 And G X 2x 4 Find F 9 X Brainly Com
G(x) = f (x k), can be sketched by shifting f (x) k units horizontally Vertical Stretches and Shrinks For the base function f (x) and a constant k > 0, the function given by g(x) = k f (x), can be sketched by vertically stretching f (x) by a factor of k if k > 1 or by vertically shrinking f (x) by a factor of k if 0 < k < 1 Horizontal Stretches and Shrinks For the base function fG(x) = 2x 1 g (x) = 2 x 1 Set up the composite result function f (g(x)) f (g (x)) Evaluate f (g(x)) f (g (x)) by substituting in the value of g g into f fF (X)= 4/ (x3) g (x)= (x2)/x solve fg (a)= 1 4/ (x3)* (x2)/x= 4x8/ x 2 3x sub in 2 3athen equate to 1 4a8/a 2 3a=1Times the bottom half of the equation up4a8=a 2 3aThe move the 4a8 across to get a 2 7a8=0Factorise (a1) (a8) Answered by Esther J • Maths tutor 2873 Views See similar Maths GCSE tutors




If F X 5x 4 And G X 4x 1 Find F G Brainly Com




If F X G X And G X F X Forall X And F 3 5 F 3 Then F
Answer to If f(x) = 3x^27, g(x) = x^24x5 find (fg)(x) By signing up, you'll get thousands of stepbystep solutions to your homeworkF (g (2)), g (x)=2x1, f (x)=x^2 \square!F(2) = 2^2 = 4 when you say f(g(x)), then the independent variable in the equation becomes g(x) g(x), however, was the dependent variable in another equation, so it's value had to be calculated before you could put it into f(g(x)) that's exactly what we did above we solved for g(2) to get 7 then we solved for f(g(x)) to get f(7) = 3 you are placing g(x) into the argument of the equation




F 4 If G X 2 X F 4 11 2 1 30 If G X 2 X 0 2 Brainly Com




Answered 23 24 How Would You Remove The Bartleby
From the chain rule of composition of functions we have (fog)'(x) = f'(g(x)) g'(x) In the given problem f(g(x)) = x^2x, therefore (f(g(x))' = 2*x1 = f · Let F, G be defined by F(x) = ∫x 0e − t2dt G(x) = ∫1 0e − x2 ( t2 1) t2 1 dt Prove that F(x)2 G(x) = π 4 I can prove that F(x), G(x) are derivable And F ′ (x) = e − x2 G ′ (x) = ∫1 0 − 2x(t2 1)e − x2 ( t2 1) dt = ∫ − 2x2 0 eudu = e − 2x2 − 1, with u = − x2(t2 1) And then I try to prove that 2FCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



Solved If F X 3x 2 And G X X 4 F G 4 Is Course Hero




If G X F X K What Is The Value Of K Brainly Com
A) 4x2 B) 4x1 C) 8x4 D) 8x1 E) 16x23 Posted October 31, 18 The way to think about this (for me, anyway) begins with understanding that 2something 3 = 8x – 1, and our job is to figure out what that something is Since this question gives us answer choices, all we really need to do is try each oneIf x is "close to" 2Solution for g (x)=4f (x) equation Simplifying g (x) = 4f (x) Multiply g * x gx = 4f (x) Multiply f * x gx = 4fx Solving gx = 4fx Solving for variable 'g' Move all terms containing g to the left, all other terms to the right Divide each side by 'x' g = 4f Simplifying g = 4f
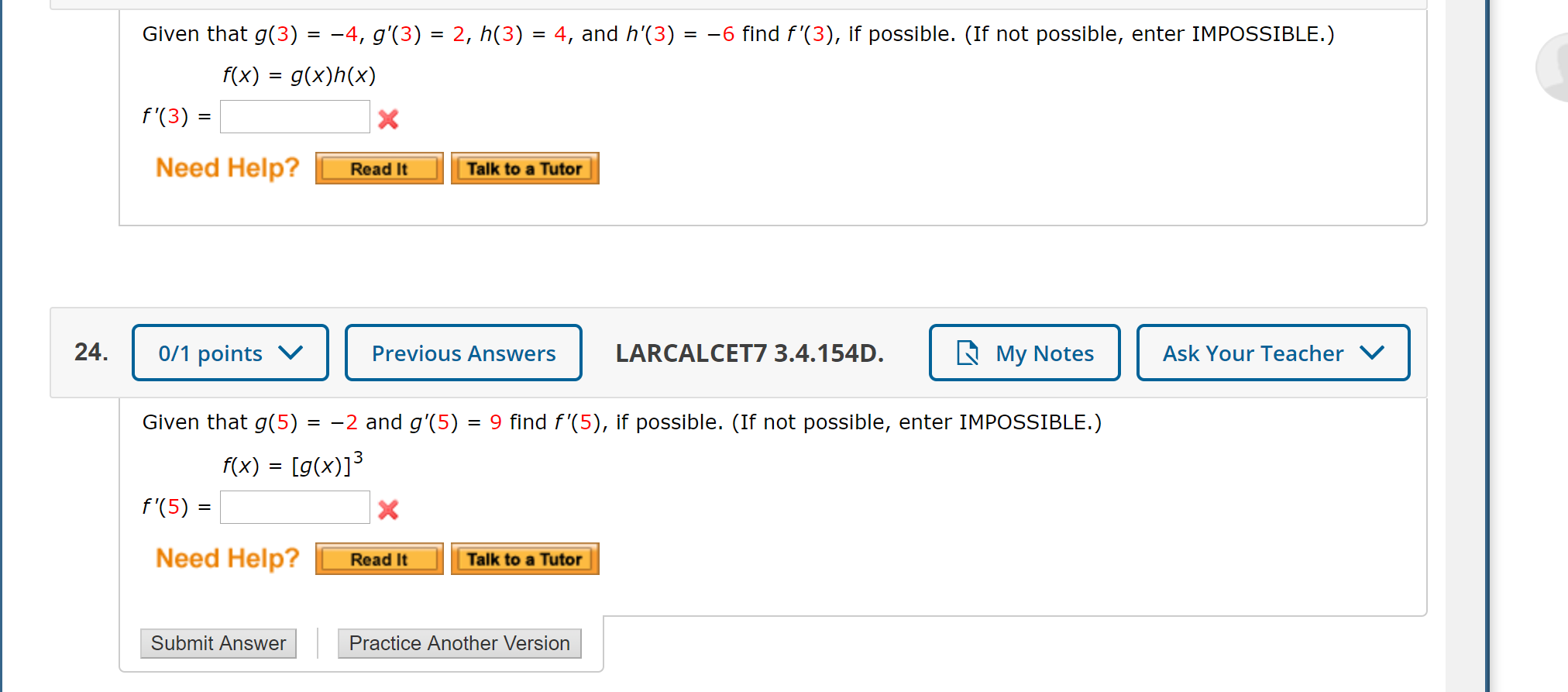



Solved Given That G 3 4 G 3 2 H 3 4 And H Chegg Com




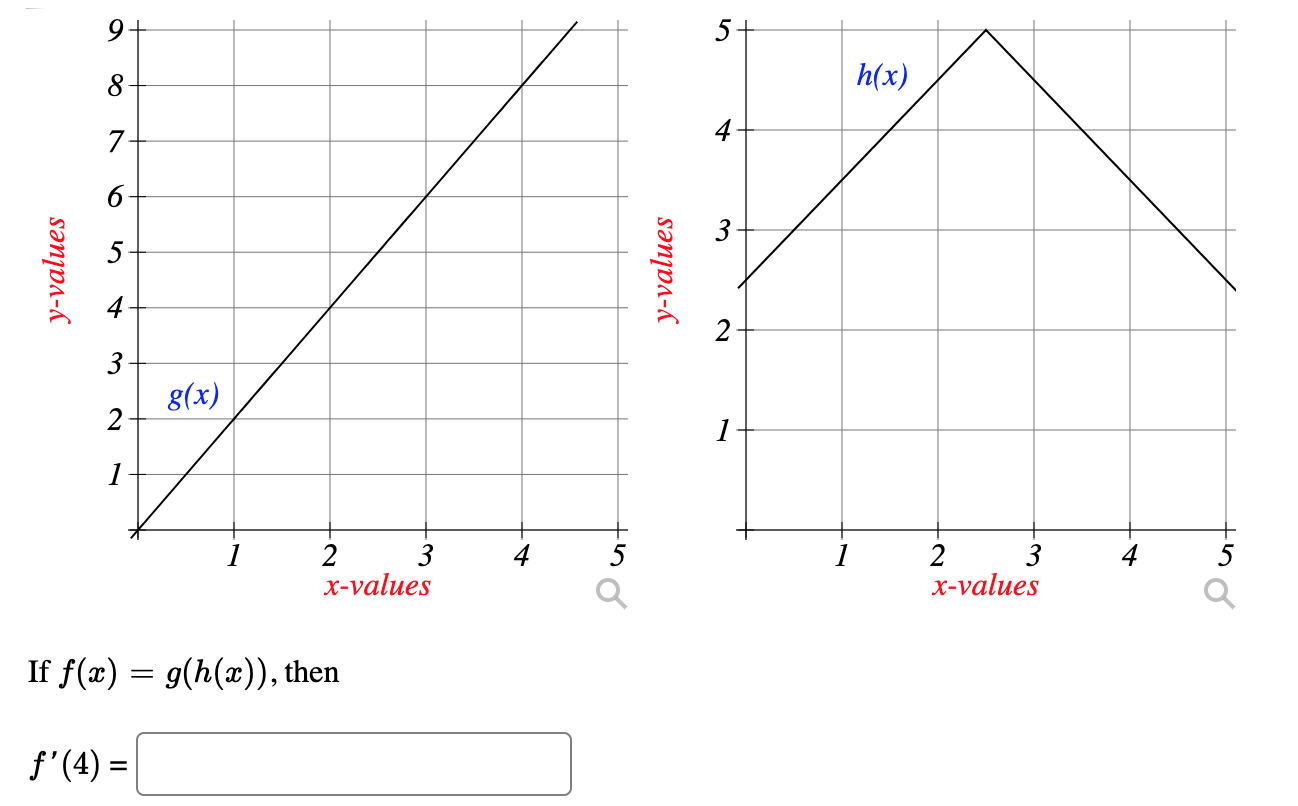
1 Point A Table Of Values For F G F And G Is Chegg Com
· f(x) = x 2 g(x) = x – 4 (f g)(x) = Get the answers you need, now!X!2 g(x) = 2(2) 0 5 = 4 5 (b) lim x!2 f(x) h(x) (c) lim x!2 f(x)h(x) g(x) Note 1 If lim x!ag(x) = 0 and lim x!af(x) = b, where bis a nite number with b6= 0, Then the values of the quotient f(x) g(x) can be made arbitrarily large in absolute value as x!aand thus 1 the limit does not exist If the values of f(x) g(x) are positive as x!ain the above situation, then lim x!a f(x) g(x) = 1, IfStack Exchange Network Stack Exchange network consists of 177 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers




If F X 1 X 1 And G X X 2 X 3 Then Number Of Points




All About Functions Chapter 2 Sections 1 Ppt Download
F (g(x)) f ( g ( x)) Evaluate f (g(x)) f ( g ( x)) by substituting in the value of g g into f f f (x2) = 3(x2)−4 f ( x 2) = 3 ( x 2) 4 Simplify each term Tap for more steps Apply the distributive property f ( x 2) = 3 x 3 ⋅ 2 − 4 f ( x 2) = 3 x 3 ⋅ 2 4 Multiply 3 3 by 2 2 f ( x 2) = 3 x 6 − 4 f ( x 2 · The graph of g(x) is the graph of f(x) reflected over the xaxis, translated 6 units to the left and shifted down 3 units Write the equation for g(x) algebra 2 The graph of g(x) is the graph of f (x)= x^2 shifted 4 units left, vertically stretched by a factor of 3, then shifted 5 units up What is the function rule for g(x)?Experts are waiting 24/7 to provide stepbystep solutions in as fast as 30 minutes!*




If F X 3x 9 2x 4 2x 3 3x 2 X Cos 5 And G X F 1 X Youtube
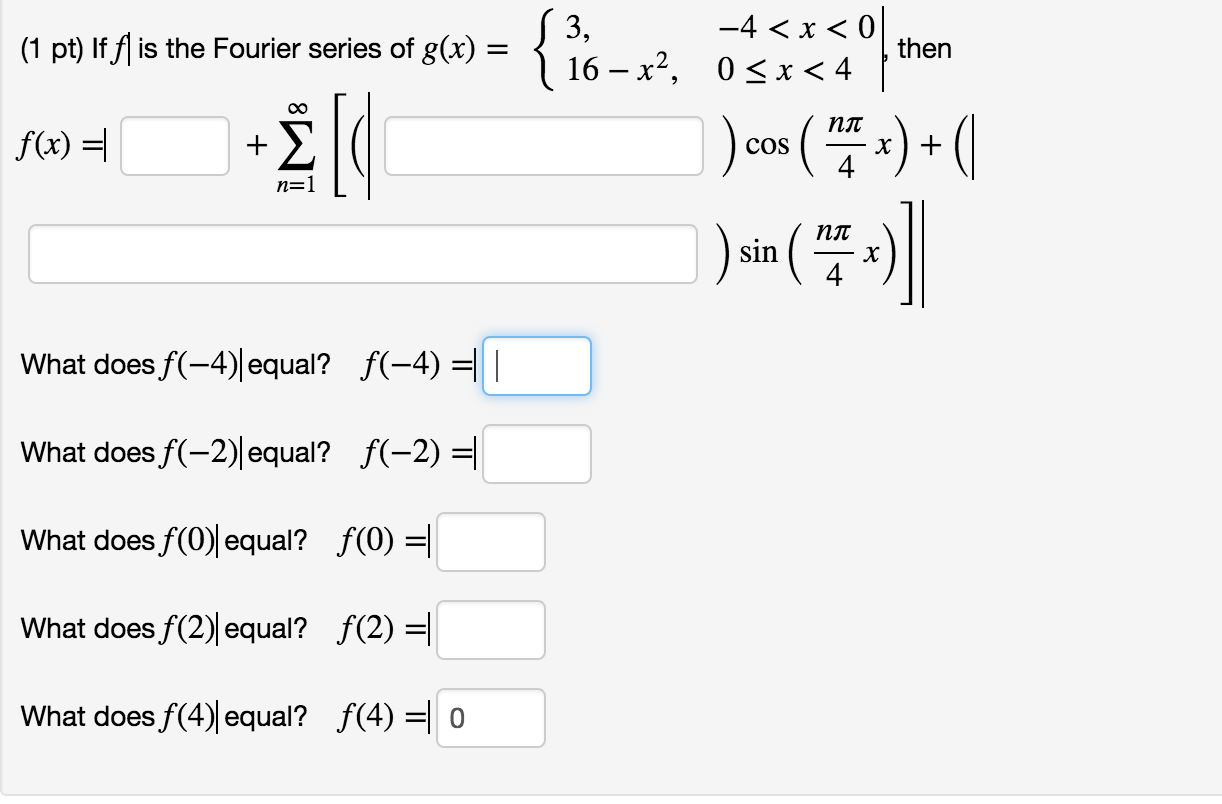



Solved If F Is The Fourier Series Of G X 3 4 X Chegg Com
Let f(x) = x 2 3 g(x) = 2x 1 Q2) Find fg(x) and explain why fg(x) = 1 has no real solution Like in Q1) we must find the function fg(x) before we solve it fg(x) = fg(x) = f(2x1) = (2x1) 2 3 If we follow the same method as before we will find that fg(x) = 1 has no real solution fg(x) = (2x1) 2 3 = 1 (2x1) 2 = 2 The next step we would usually take is to square root the numberSolution for Let f(x) = x2 x 4 and g(x) = 2x 6Find g(f(1)) Want to see this answer and more?(g ∘ f)(x) = g(f(x)) = g(2x 4) = (2x 4) 3 If an airplane's altitude at time t is a(t), and the air pressure at altitude x is p(x), then (p ∘ a)(t) is the pressure around the plane at time t Properties The composition of functions is always associative—a property inherited from the composition of relations That is, if f, g, and h are composable, then f ∘ (g ∘ h) = (f ∘ g



Solved If G 3 4 And H 3 1 Find F 3 For F X 5g X 3h X 2 A 19 B 17 C 23 D 25 Course Hero




Let F 5 5 Rarrr Be A Differentiable Function Of With F 4 1




Test 1 Review




What S F G 4 If F X 3x2 3x 6 And G X 2x Oa 210 B 174 C 12 Od 24 Brainly Com




3 Math275lab3 Questions And Answers Studocu




Solved If F Is The Fourier Series Of G X 3 4 X Chegg Com




Onudeuepyvmlom




F 4 If G X 2 X Brainly Com




Solved 1 Point Let F X F F X And G X F X 2 An Chegg Com




If F X And G X Are Two Functions With G X X 1 X And F G X




If F X X And G X X Then Value Of Gof 5 4 Is Teachoo




If F X 3x2 2x 4 And G X 5x2 6x 8 Find F G X Brainly Com




F 4 If G X 2 X Brainly Com




Solved 5 Suppose That F X And G X Are Differentiable F Chegg Com




If G X X 2 X X 1 And G F X 4x 2 10x 5 Then Find F 5 4




If G X 1 2f X Which Of The Following Are Solutions To G X Brainly Com




Document




If G X X 2 X 2 And 1 2 Gof X 2x 2 5x 2 Then F 1 X



Solved pc Unit 4 Functions 4 Functions H X 2x 3 The Graphs Of The Functions F And G Are Given Below K X X 3x 5 M X 4 X If X53 Course Hero




Inverse Derivative Problems Key




Simplify If Fx Frac X2 2x 3x2 3x 4 And Gx Frac 3 Gauthmath




If G X F X F X 0 X 4 3 F X F X Cos X X 4 2x F X F



Answered If Fx 1 X 2 And G X 4 X Find Bartleby
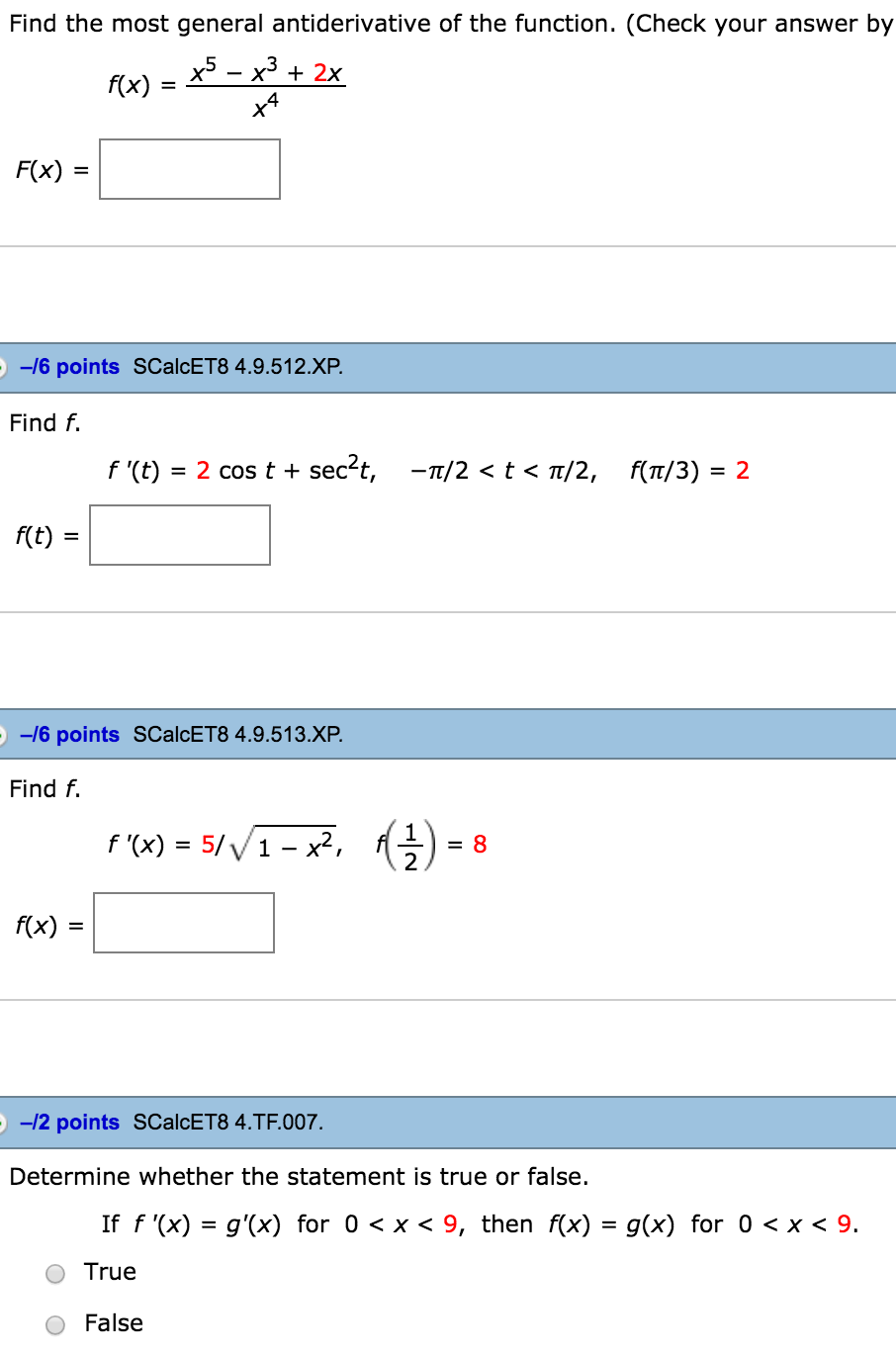



Solved Find The Most General Antiderivative Of The Functi Chegg Com




What Is The Value Of G F X




If F




If F X 5x 7 And G X 2x 4 Find F G X X Brainly Com




If F X 2x 9 And G X 4x 2 5x 3 Find F O G And G O F Brainly In



Unit 17 More Algebra Mathematics 9 1 Igcse Year Ppt Download
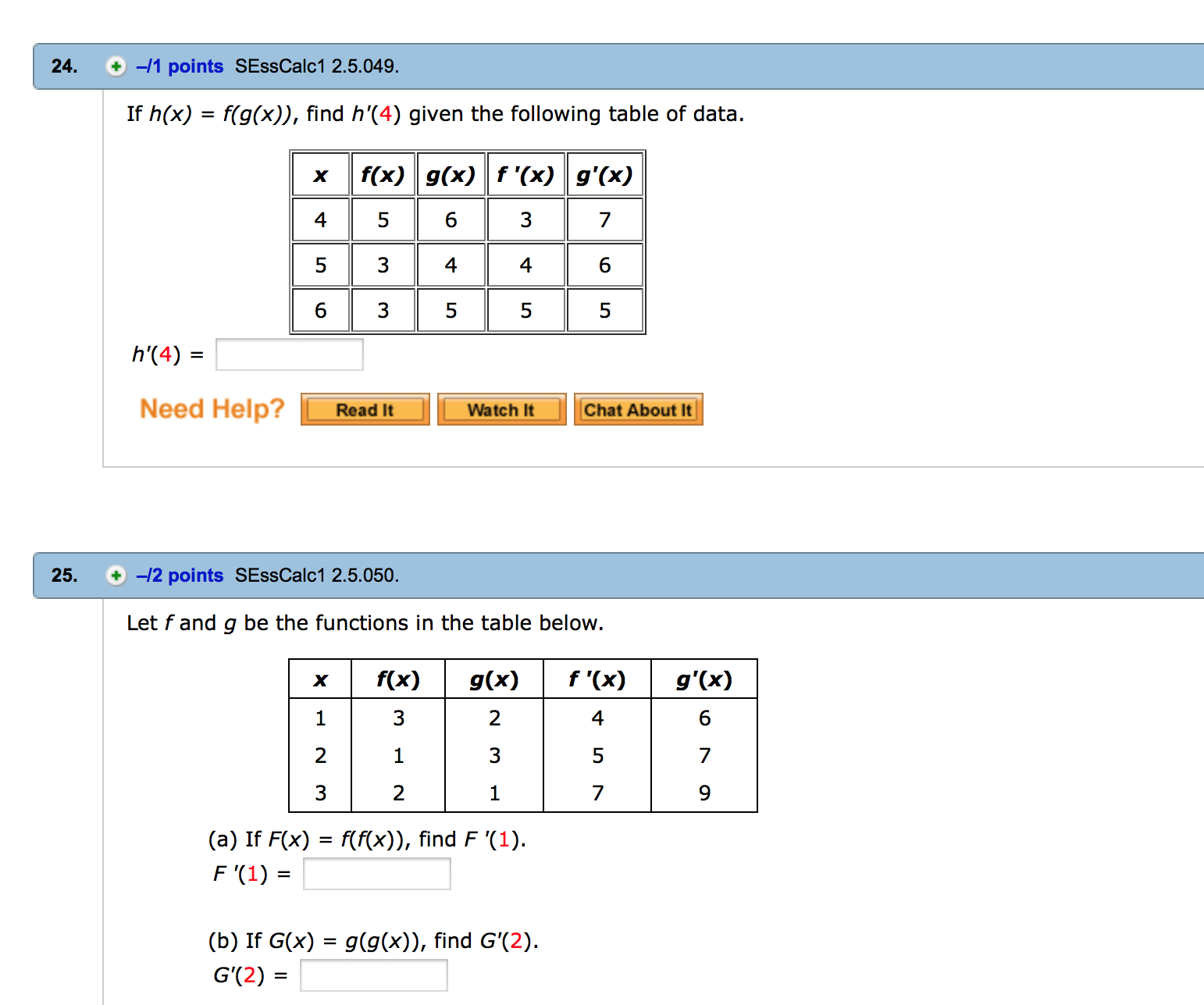



If H X F G X Find H 4 Given The Following Chegg Com




Find F G X If X X 2 3 And G X 4x 2 X 4 Brainly Com




If The Function F X Has A Domain Of 2 X 8 And A Range Of 4 Y 6 And The Function G X Is Defined By The Formula G X 5f 2x Then What Are




If F X X2 G X 2x And H X X 4 Then Prove That Fo Goh Fog Oh Brainly In



Solved Given F X 2x 4 And G X 1 2 2 Use The Definition Of Inverses To Determine If F And G And Inverses Course Hero




Revision
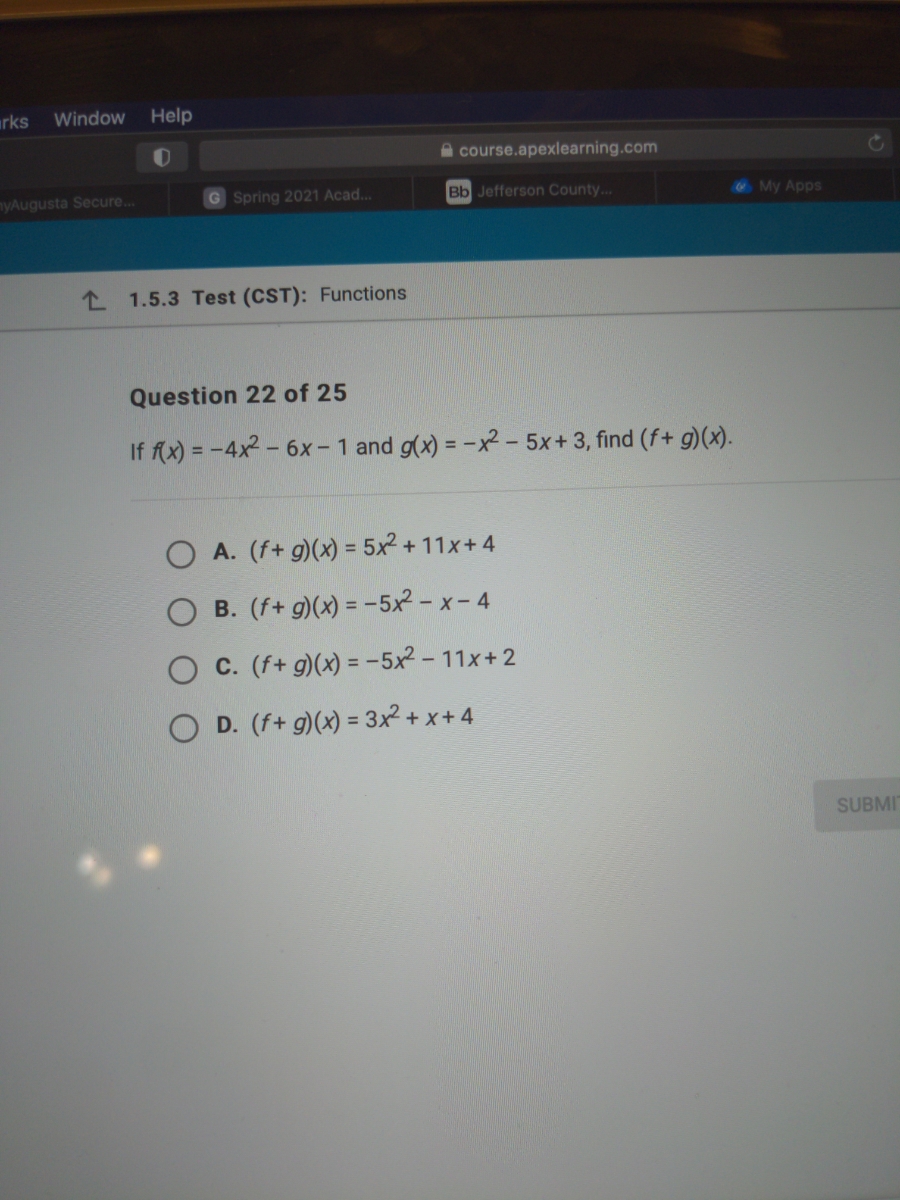



Answered Question 22 Of 25 If Fx 4x2 6x 1 Bartleby




Solved If G X 2x Integral Tan X 0 1 Squareroot1 T 2 Chegg Com




Ans Fx F 4 K 2 3 If Fx X 3 2 And Gx 2x 3 P Gauthmath




Te Directions A Determine Whether The Following Gauthmath
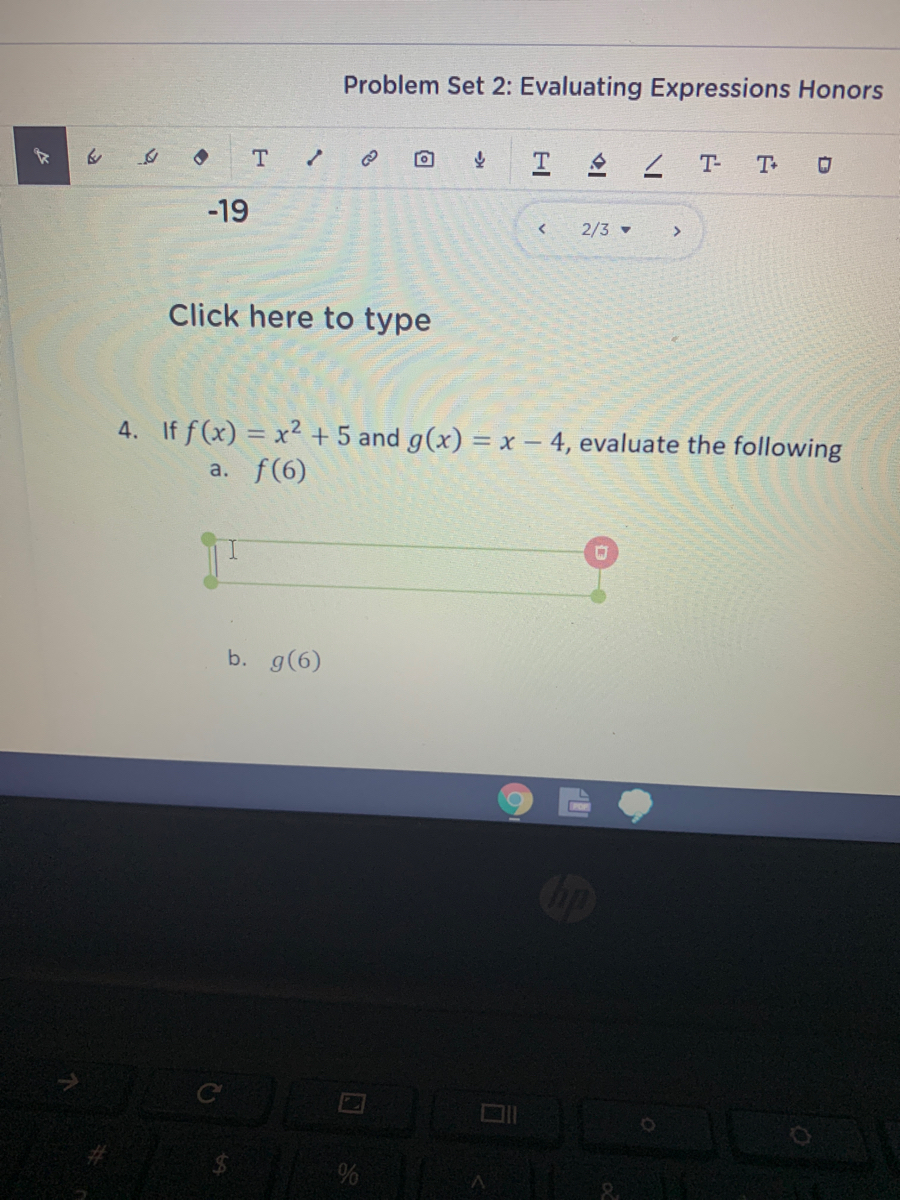



Answered If F X X 5 And G X X 4 Bartleby
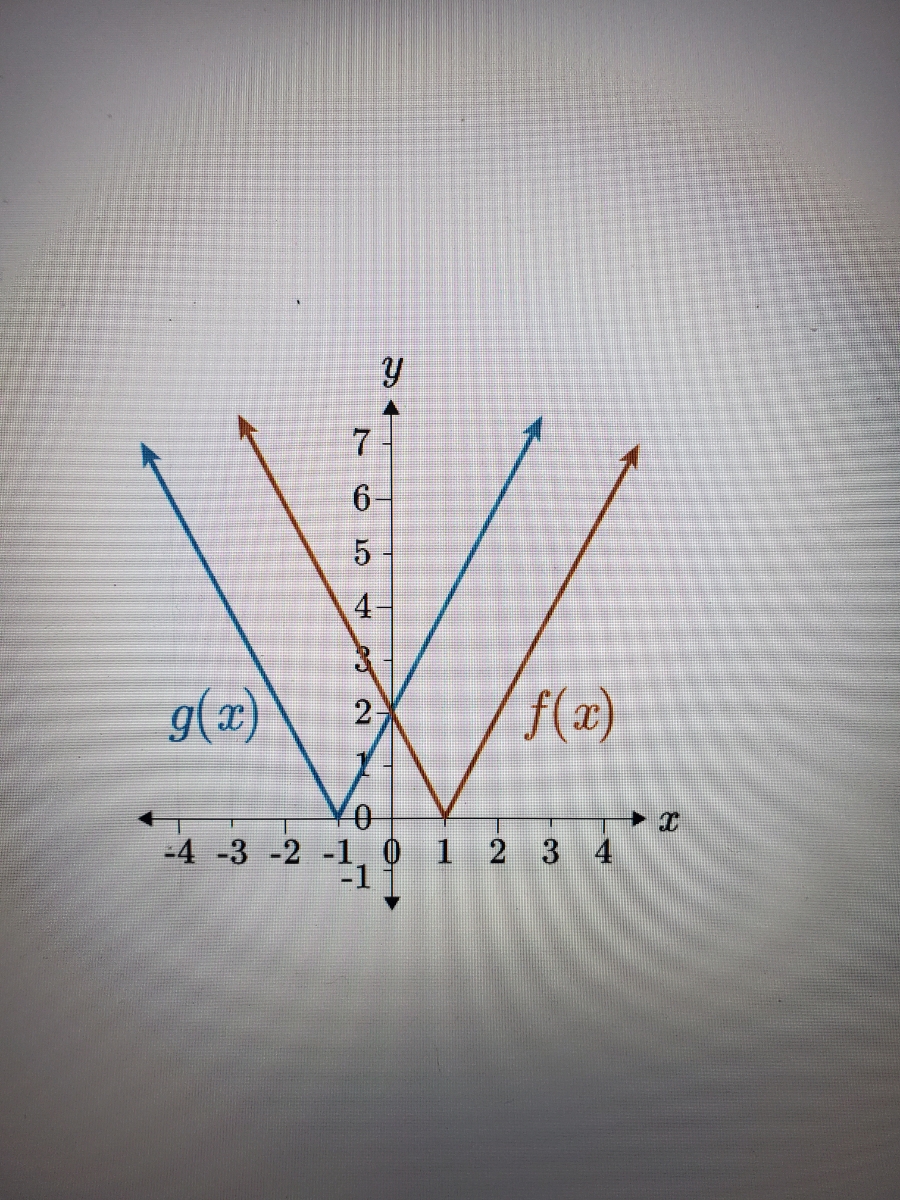



Answered The Graph Shows The Functions F X Bartleby




F 4 If G X 2 X Brainly Com




Wir 8




Answered C X Ll 3 2 Given F A Find Bartleby




For Questions 1 2 Use The Following Functions F X 3x 7 G X 2x 4 1 Find F G X 2 Brainly Com




If G X Frac 12 Frac 19 X 2 4 2 Is Obtained By Doing G X F Kx Horizontal Stretch Of Function F What Is Number K Mathematics Stack Exchange




If F X E G X And G X Int 2 X Dt 1 T 4 Then F




If F X X And G X X Then Value Of Gof 5 4 Is Teachoo
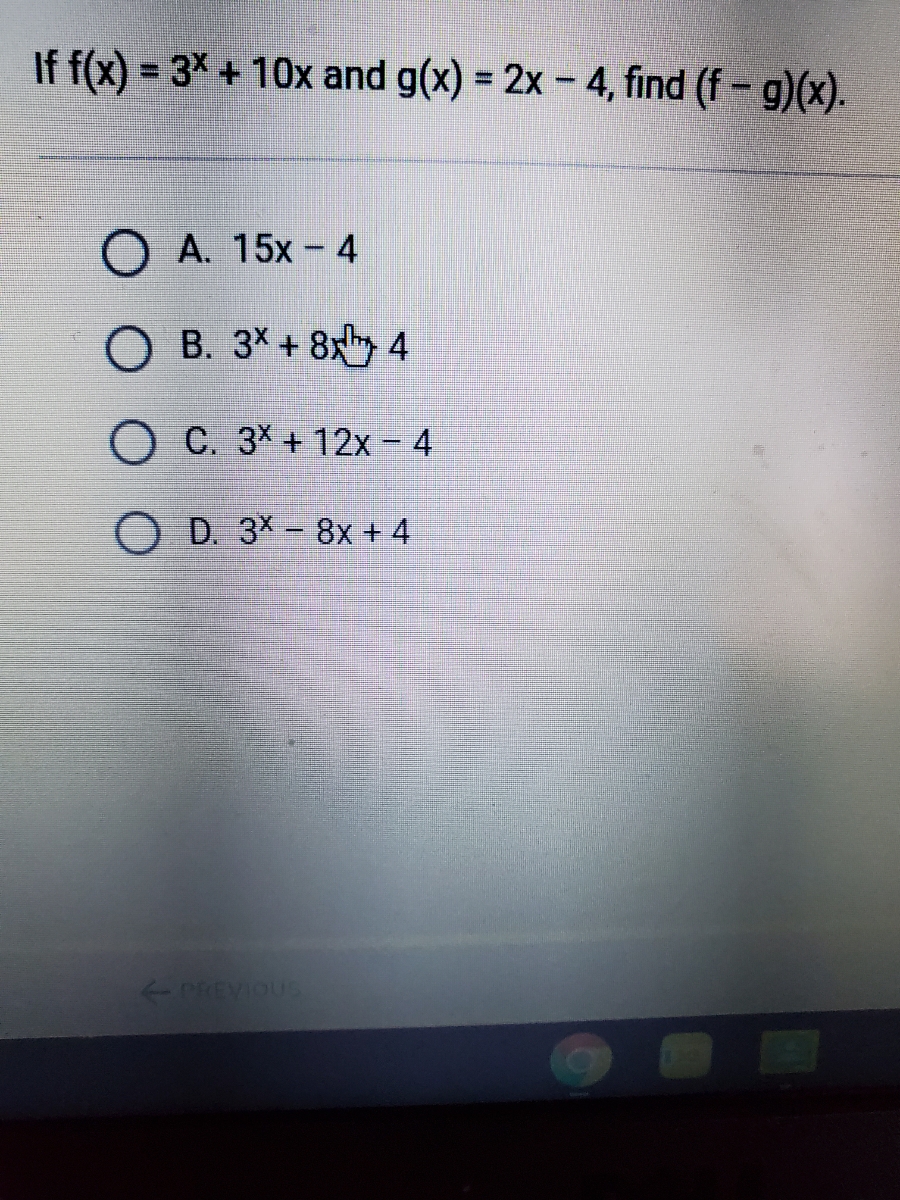



Answered If F X 3 10x And G X 2x 4 Bartleby




Warm Up In The Composite Function M D X Function D Is Called The Function Give Another Symbol For M D X If F X 2x And G X X Ppt Download




Answered Given That Lim F X 4 Im G X 4 Bartleby




If F X G X G X 2 2 H X H X 1 Where G And H




1 For A Function F Use The Fact That F 3 12 Chegg Com




Are Inverses F X




1 If F X 3 As X 4 Then F 4 3 True B False Chegg Com




Question Video Evaluating Composite Functions At A Given Value Nagwa
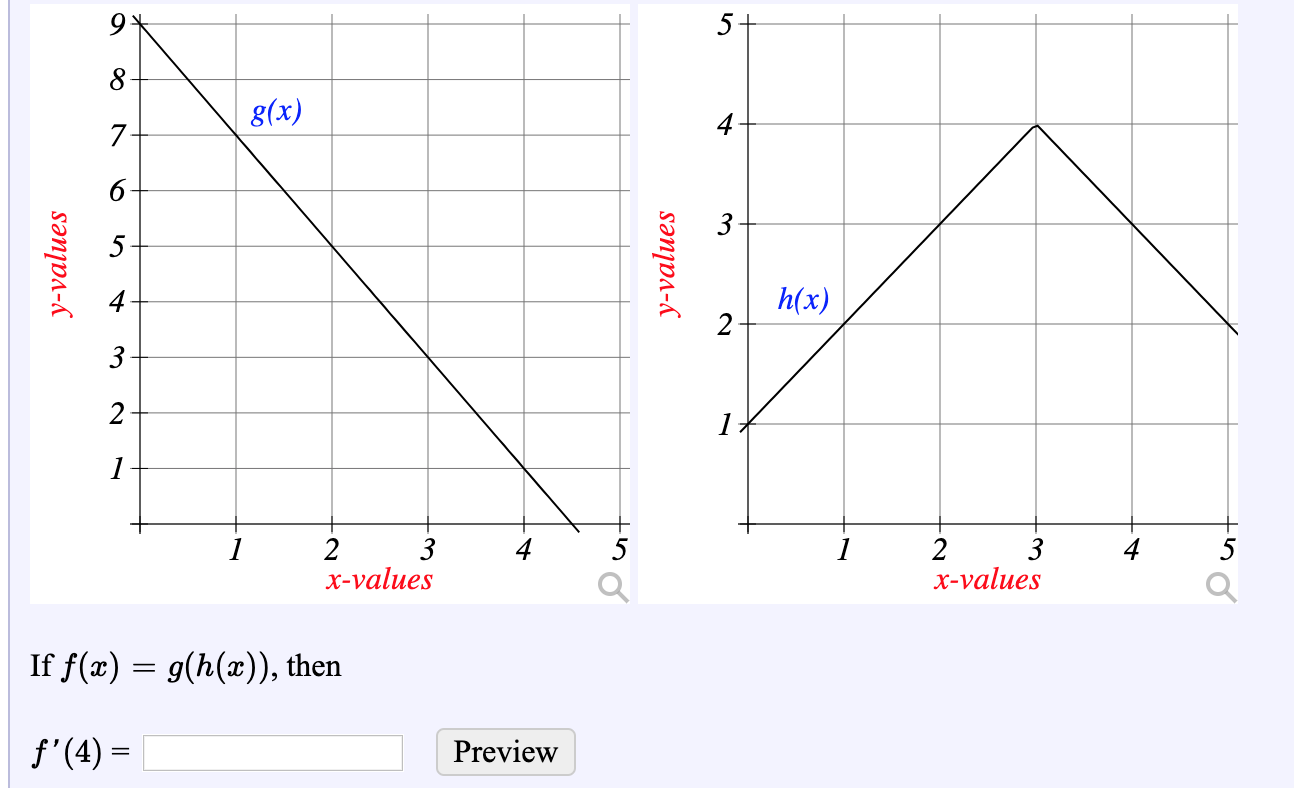



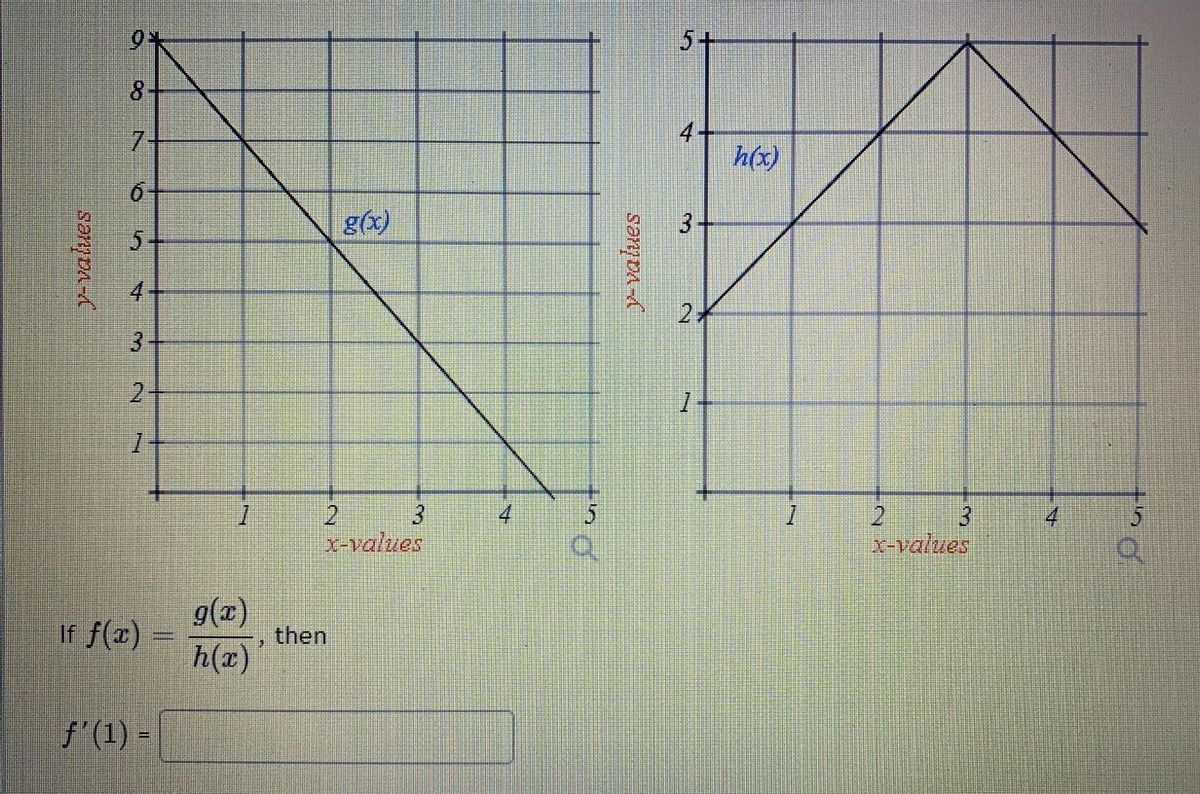
Solved 9 5 8 G X 4 7 6 5 H X 2 4 3 2 1 1 2 3 H Value Chegg Com




Function Notation Direct Variation
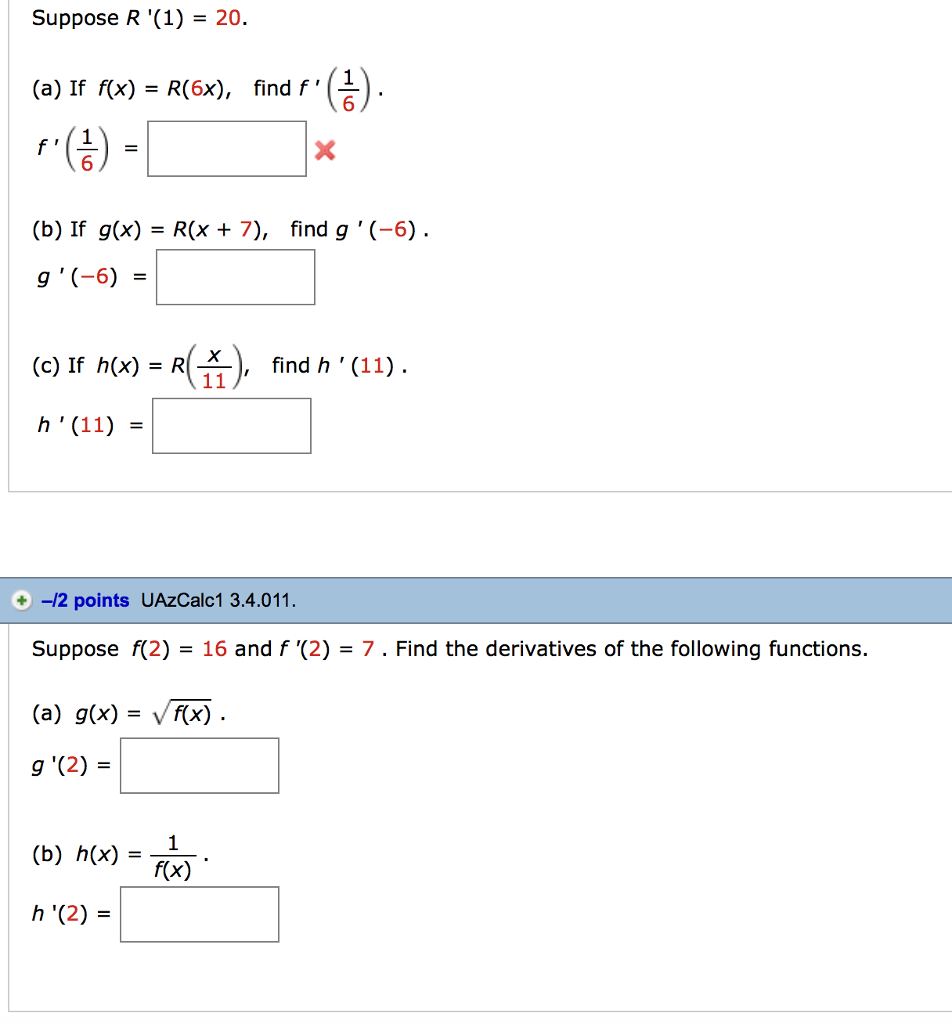



Suppose R 1 If F X R 6x Find F 1 6 Chegg Com




If F X 5 4 And G X 3 2 Find F G X Brainly Com




Answered Continuous Extensions 41 Define G 3 Bartleby



0 件のコメント:
コメントを投稿